Create following classes:
- Node which stores the integer value (key) and links to its left and right child
- BST maintains the binary search tree built with Node classes.
Create following methods for class BTS:
- insert(key: int): inserts a new key to the search tree, no duplicates.
- search(key: int): searches the key from the search tree and returns boolean True if the value is found, False otherwise.
- preorder(): prints the content of the search tree in preorder. Implement the method using recursion.
A code template with an example program:
class Node:
# TODO
class BST:
# TODO
if __name__ == "__main__":
Tree = BST()
keys = [5, 9, 1, 3, 7, 4, 6, 2]
for key in keys:
Tree.insert(key)
Tree.preorder() # 5 1 3 2 4 9 7 6
print(Tree.search(6)) # True
print(Tree.search(8)) # False
Submit your solution in CodeGrade as bintree.py.
Assignment 5.2: Removing a Node (3 points)
Add new method remove(key: int) to the BST class. The function removes the node which has the given key value while maintaining the binary search tree property.
An example program:
if __name__ == "__main__":
Tree = BST()
keys = [5, 9, 1, 3, 7, 4, 6, 2]
for key in keys:
Tree.insert(key)
Tree.preorder() # 5 1 3 2 4 9 7 6
Tree.remove(1)
Tree.preorder() # 5 3 2 4 9 7 6
Tree.remove(9)
Tree.preorder() # 5 3 2 4 7 6
Tree.remove(3)
Tree.preorder() # 5 2 4 7 6
Submit your expanded version of bintree.py in CodeGrade.
Assignment 5.3: Breadth-First Enumeration (2 points)
Breadth-First enumeration presents the nodes of the search tree level by level (or depth) unlike preorder
enumeration which presents the left subtree completely before the right subtree.
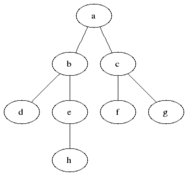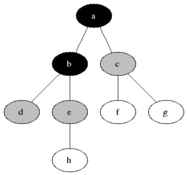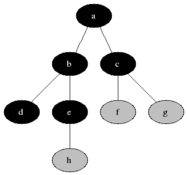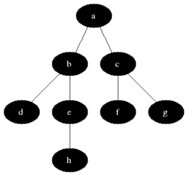
Figure 1: Breadth-First enumeration for a binary tree. Black: explored, grey: queued to be explored later on (source: wikipedia.org).
Add a new method breadthfirst() to the BST class which prints out the content of the search tree in breadth-first order.
An example program:
if __name__ == "__main__":
Tree = BST()
keys = [5, 9, 1, 3, 7, 4, 6, 2]
for key in keys:
Tree.insert(key)
Tree.preorder() # 5 1 3 2 4 9 7 6
Tree.breadthfirst() # 5 1 9 3 7 2 4 6
Submit your expanded version of bintree.py in CodeGrade.